a)     Programme

Electrostatique.

Exercices :

b)     Unité d’enseignement : UE 1                                                                         1ere Année

Matière : Physique  Module  P1 : Fondamentaux de Physique

Volume horaire : 30 heures  Cours=10h/TD=16h/TP=4h

 

Objectifs et compétences minimales 

Connaître les caractéristiques des composantes de bases et la définition d’une onde électromagnétique.

Etre capable de :

·        maîtriser les notions de base de la propagation.

·        caractériser les composants discrets de base.

Contenu :

·        Résistance, condensateur, inductance…

·        Définition des composants

 

Modalités de mise en œuvre :

Utilisation de ressources multimédia pour illustrer les phénomènes physiques

Electrostatique.

 

1     Loi de Coulomb.

1.1     Charges électriques.

On trouve 2 types de charges électriques que par commodité on note négatives et positives (On aurait pu les appeler vertes et rouges).

1.2     Direction et sens des forces électriques.

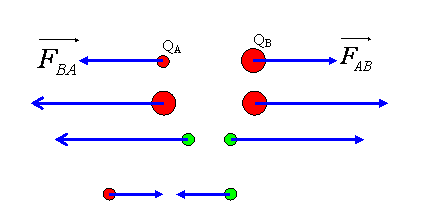
Si deux charges QA et QB  de même signe (toutes deux positives ou toutes deux négatives) sont situées aux points A et B :

La charge située en B est soumise à une force  dirigée selon le vecteur .

signifie force appliquée à QB et causée par QA.

La charge située en A est soumise à une force  dirigée selon le vecteur .

Les forces F BA et F AB sont égales et opposées.

 

Si les charges sont de signes contraires :

La charge située en B est soumise à une force  dirigée selon le vecteur.

La charge située en A est soumise à une force  dirigée selon le vecteur.

Dans les deux cas les forces et  ont même module et sens opposés.

 

1.3     Intensité des forces électriques : loi de Coulomb.

Les expériences montrent que les intensités des forces auxquelles sont soumises les charges situées en A et B sont:

 

 est le vecteur unitaire de même direction et de même sens que

     et          

Les signes de QA et QB permettent de tenir compte du changement de sens des forces dans le cas de charges de type différents.

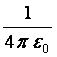est un coefficient permettant de tenir compte des unités légales (U.S.I. = unité du système international).

F          en newtons :     N

Q         en coulombs :   C

r           en mètres :       m

 est appelée : permittivité du vide en farads/mètre : F/m

Valeurs numériques :

la relation :  se retient aisément et on a μ0 = 4 π 10-7 et c = 3.108 m/s

 = 8,85.10-12  donc :  

 

1.4     Analogie avec la gravitation.

 

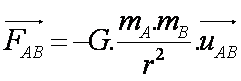
 avec G appelée constante d'attraction universelle :  G = 6,67.10-11 U.S.I.

 

2     Notion de champ électrique.

2.1     Définitions.

On peut considérer qu’il existe une partie de l’espace dans laquelle une charge ponctuelle q sera soumise à une force , cette force dépend de q mais aussi de ce qui existe dans cette partie de l’espace.

On dit que l’on a affaire à un champ électrique (ou électrostatique), on peut écrire :

Le champ électrique  est donc un champ vectoriel.

Dans le cas d’un charge ponctuelle Q placée en l’origine O , calculons le champ en un point M

¨     Ligne de champ dans le cas d’une seule charge

On appelle "ligne de champ" une ligne telle qu'en tout point M de la ligne le champ électrique E( M ) mesuré au même point lui est parallèle ; dans le cas présent la symétrie sphérique de la charge et de l'espace entraîne que toutes les lignes de champ soient des droites qui passent par cette charge . Ces lignes de champ sont orientées dans la direction opposée à la charge si celle ci est positive .

¨     Principe de superposition

Dans le vide il y a addition vectorielle des champs créés par plusieurs charges ponctuelles.

voir : http://www.colorado.edu/physics/2000/waves_particles/wavpart3.html

et aussi  Champelec\Champelec.htm  (auteur  Sadahisa Kamikawa kamikawa@vir.bekkoame.or.jp )

 

2.2     Distributions ponctuelles de charges.

Dans le cas de plusieurs charges, on fait la somme vectorielle du champ créé par chaque charge (dans le vide)

 

Exemple : soit 3 charges QA QB et QC placées en A B et C, le champ électrique en un point M s’exprime par :

 

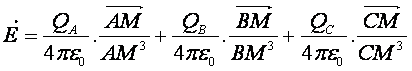
Soit dans le cas général où on a N charges Q1 Q2 Q3 ……QN placées aux points P1 P2 P3 ….PN :

 

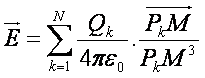
2.3     Dipôle électrique

On appelle dipôle électrique un ensemble formé de deux charges -q (en N) et +q (en P) de mêmes valeurs absolues et de signes contraires.

L'ensemble formé des deux charges reste globalement neutre.

Le dipôle est défini par la charge q et par le vecteur NP qui joint les deux charges.

On appelle moment dipolaire le vecteur

 

2.4     Distributions réelles de charges.

La formule : 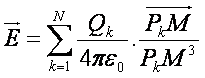va se transformer en :

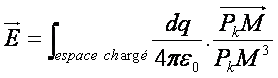
répartition linéïque : où dl représente un élément de longueur

répartition surfacique :  où dS représente un élément de surface

répartition volumique :   où dτ représente un élément de volume.

3     Potentiel électrique.

Le champ électrique est un champ vectoriel, c'est-à-dire qu'il est caractérisé en chaque point M de l'espace par un vecteur  dont il faut connaître la direction, le sens et l'intensité.

Dans un repère orthonormé, il est repéré par ses trois composantes scalaires :

Pour déterminer le champ électrique total en un point de l'espace, il faut, en vertu du principe de superposition, faire la somme vectorielle de champs électriques élémentaires dus à chacune des charges.

Tout serait tellement plus facile si chaque point de l'espace était caractérisé non pas par un vecteur mais par un scalaire V(M), et si à partir de ce scalaire on pouvait calculer simplement le champ électrique et la force exercée sur une charge q située en ce point.

Ce champ scalaire  s'appelle le potentiel électrique.

Dans un repère orthonormé cartésien, les composantes du champ électrique sont liées à ce potentiel électrique par trois relations:

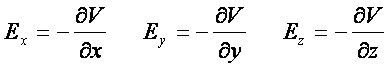
Le vecteur dont les composantes sont les dérivées spatiales d’un scalaire est appelé gradient :

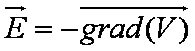
Dans un repère orthonormé  :

 

3.1     Théorème de Gauss : 

Notion de flux.

 

Cas pratique.

Lorsque le champ est perpendiculaire à la surface S et de module constant E sur cette surface, le flux s’écrit simplement :

Utilisation du théorème de Gauss.

Pour utiliser le théorème de Gauss, il faut tirer parti des propriétés de symétrie ou de disposition des lignes de champ et choisir une surface telle que le flux soit très simple à calculer.

 

Résumé.

Champ électrique créé en un point M par une charge ponctuelle Q placée en O :

                                    

 

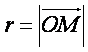
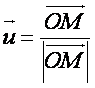
Relation entre champ et potentiel :

 

Le potentiel en un point M par une charge ponctuelle Q placée en O :

            

 

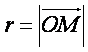
Théorème de Gauss :